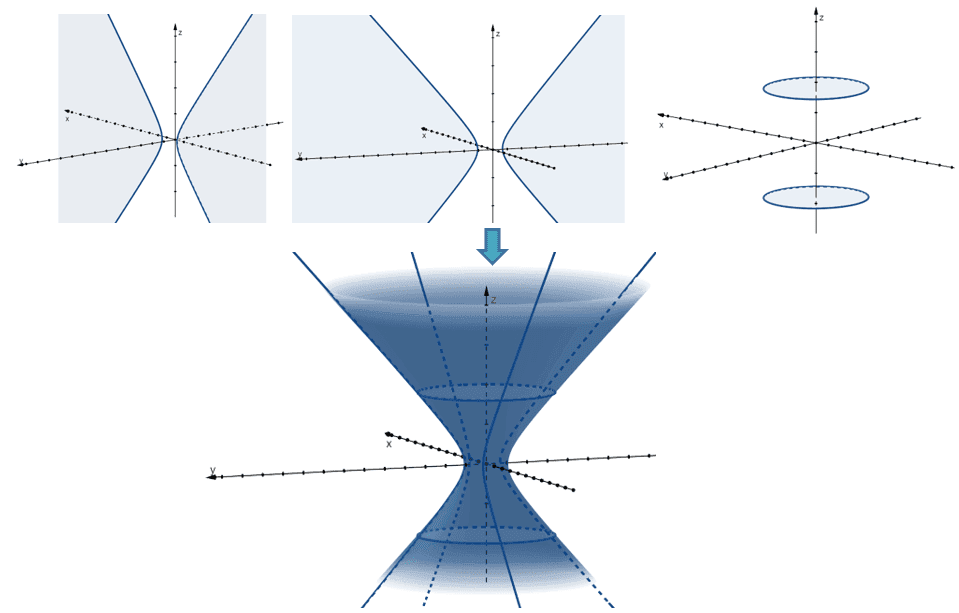
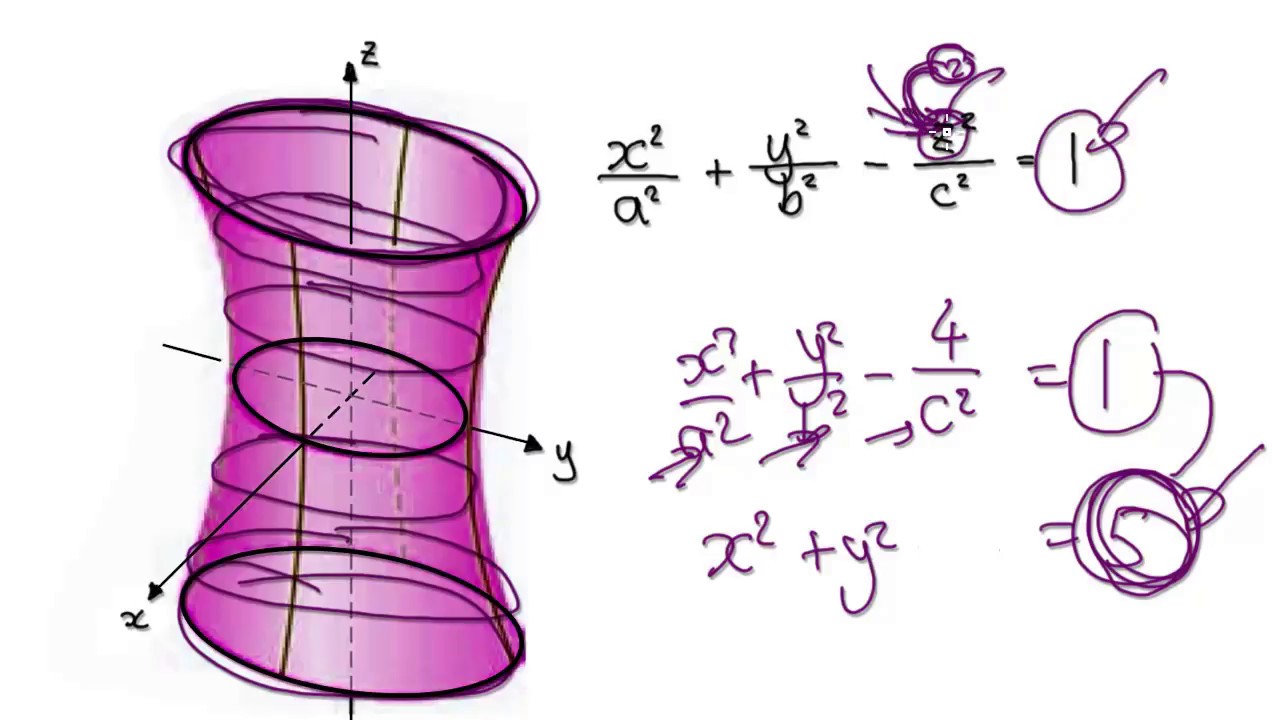
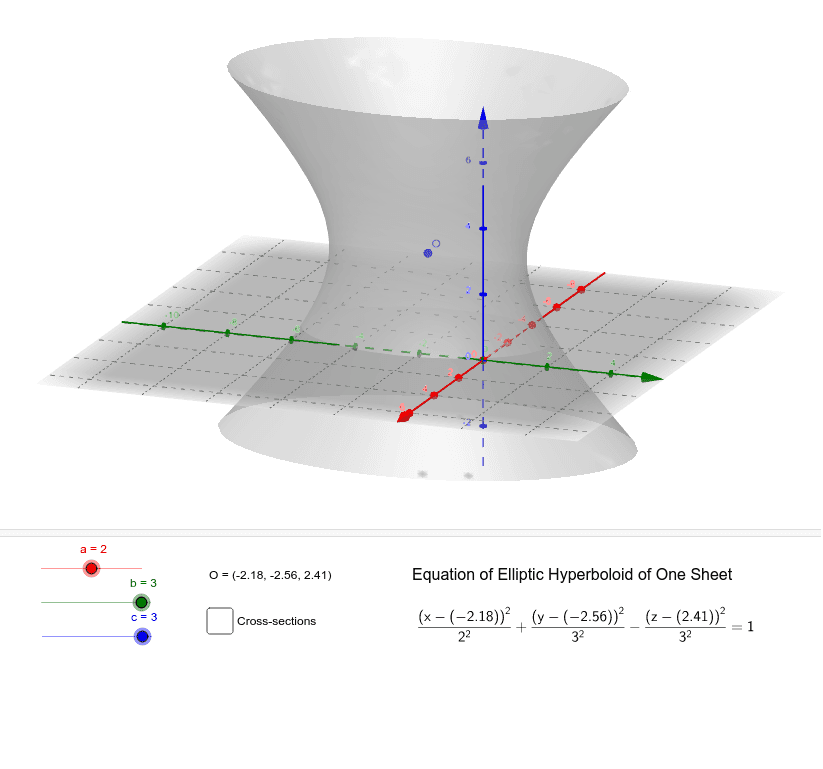
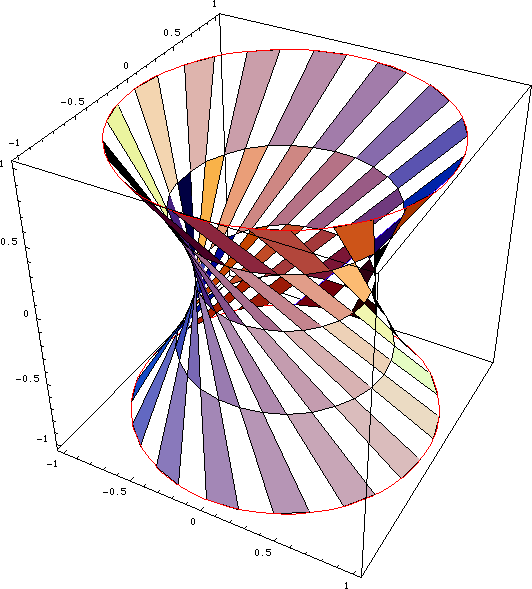One Sheet Hyperboloid Equation - The horizontal cross sections are ellipses — circles,. Here is the equation of a hyperboloid of one sheet. The diameter at the base is 280 m. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
Here is the equation of a hyperboloid of one sheet. The diameter at the base is 280 m. The horizontal cross sections are ellipses — circles,. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet.
The horizontal cross sections are ellipses — circles,. Here is the equation of a hyperboloid of one sheet. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. The diameter at the base is 280 m. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).
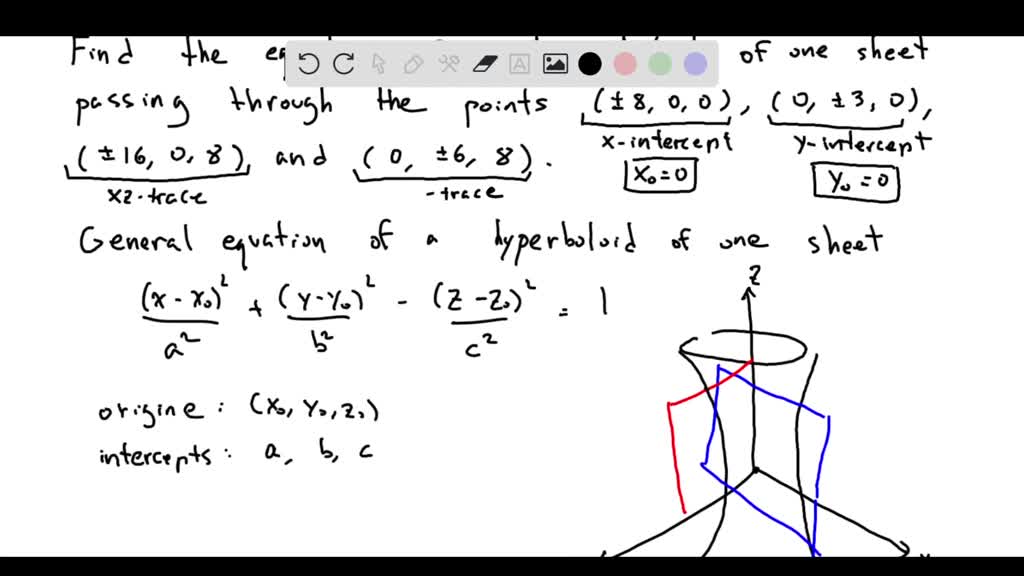
SOLVED Find the equation of the hyperboloid of one sheet passing
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. Here is the equation of a hyperboloid of one sheet. The diameter at the base is 280 m. The horizontal.
Quadric surfaces Definition, Types, and Examples
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). The horizontal cross sections are ellipses — circles,. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. Here is the equation of a hyperboloid of one sheet. The diameter.
Quadric Surfaces (Identified and Explained w/ Examples!)
Here is the equation of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). The diameter at the base is 280 m. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. The horizontal.
Video 2962 Calculus 3 Quadric Surfaces Hyperboloid of one sheet
The diameter at the base is 280 m. Here is the equation of a hyperboloid of one sheet. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. The horizontal cross sections are ellipses — circles,. A hyperboloid of one sheet is any surface that can be described with an.
Graphing a Hyperboloid of One Sheet in 3D YouTube
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. Here is the equation of a hyperboloid of one sheet. The diameter at the base is 280 m. The horizontal.
Hyperboloid of One Sheet
A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Here is the equation of a hyperboloid of one sheet. The horizontal cross sections are ellipses — circles,. The diameter at the base is 280 m. A cooling tower for a nuclear reactor is to be constructed in the shape.
Quadric Surface The Hyperboloid of One Sheet Vector Calculus YouTube
The diameter at the base is 280 m. The horizontal cross sections are ellipses — circles,. Here is the equation of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). A cooling tower for a nuclear reactor is to be constructed in the shape.
Elliptic Hyperboloid of One Sheet GeoGebra
The horizontal cross sections are ellipses — circles,. Here is the equation of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. The diameter.
QuadraticSurfaces
The diameter at the base is 280 m. The horizontal cross sections are ellipses — circles,. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). Here is the equation.
Chapter 12Section6 Quadric Surfaces ppt video online download
The diameter at the base is 280 m. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\). The horizontal cross sections are ellipses — circles,. Here is the equation.
The Diameter At The Base Is 280 M.
The horizontal cross sections are ellipses — circles,. Here is the equation of a hyperboloid of one sheet. A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet. A hyperboloid of one sheet is any surface that can be described with an equation of the form \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}−\dfrac{z^2}{c^2}=1\).