Two Sheeted Hyperboloid - Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. It’s a complicated surface, mainly because it comes in two pieces. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called.
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but.
It’s a complicated surface, mainly because it comes in two pieces. All of its vertical cross sections exist — and are hyperbolas — but. For this reason, the surface is also called an elliptic hyperboloid. Is there a way to. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called.
Graphing a Hyperboloid of Two Sheets in 3D YouTube
Is there a way to. For this reason, the surface is also called an elliptic hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. All of its vertical cross.
Quadric Surface The Hyperboloid of Two Sheets YouTube
It’s a complicated surface, mainly because it comes in two pieces. For this reason, the surface is also called an elliptic hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. Is there a way to. All of its vertical cross sections exist — and are hyperbolas — but.
Hyperboloid of Two Sheet
If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. It’s a complicated surface, mainly because it comes in two pieces. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. For this reason, the surface is also called an elliptic.
Hyperboloid of TWO Sheets
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there a way to. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. It’s a complicated surface, mainly because it comes in two pieces. All of its vertical cross.
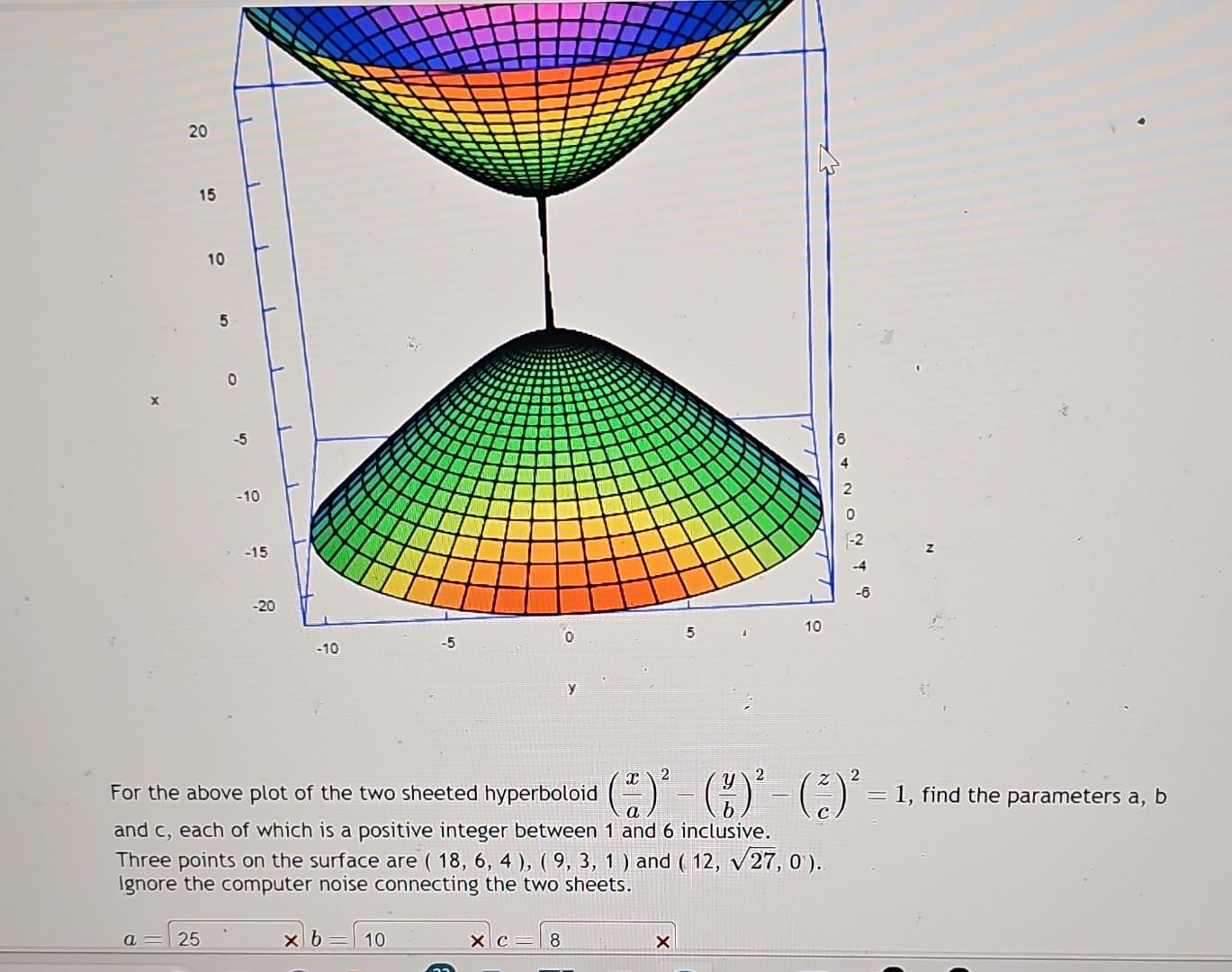
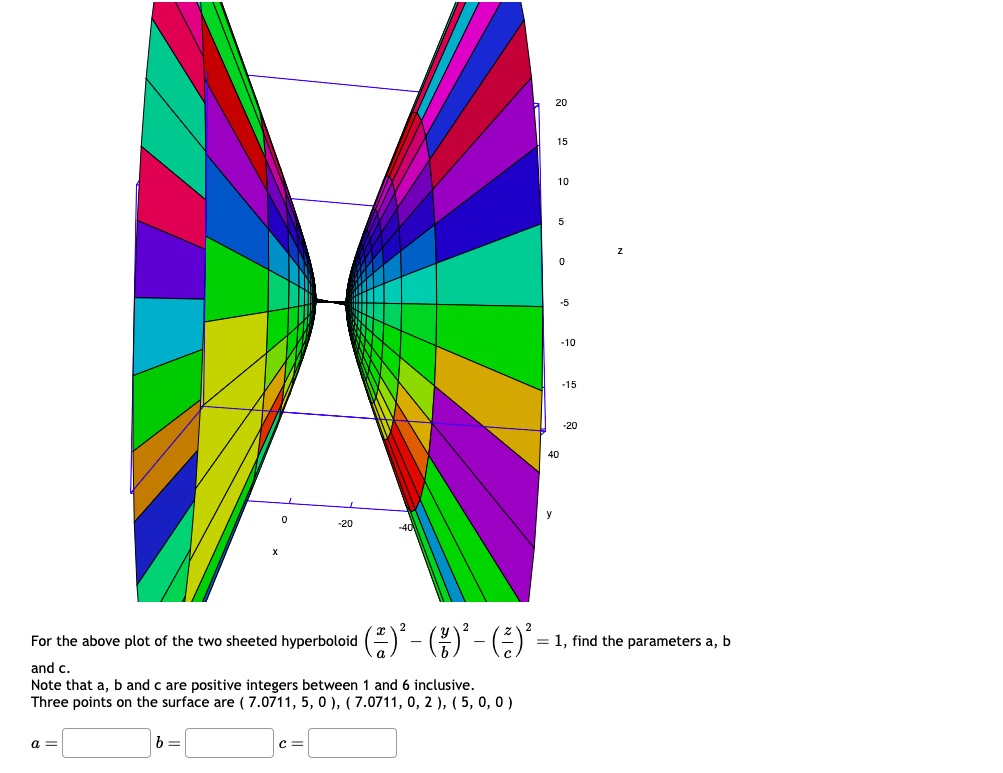
Solved For the above plot of the two sheeted hyperboloid
Is there a way to. It’s a complicated surface, mainly because it comes in two pieces. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. All of its vertical cross.
Hyperbolic Geometry and Poincaré Embeddings Bounded Rationality
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. All of its vertical cross sections exist — and are hyperbolas — but. It’s a complicated surface, mainly because it comes in two pieces. For this reason, the surface is also called an elliptic hyperboloid. Is there.
Solved For the above plot of the two sheeted hyperboloid
If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. All of its vertical cross sections exist — and are hyperbolas — but. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there a way to. For this reason,.
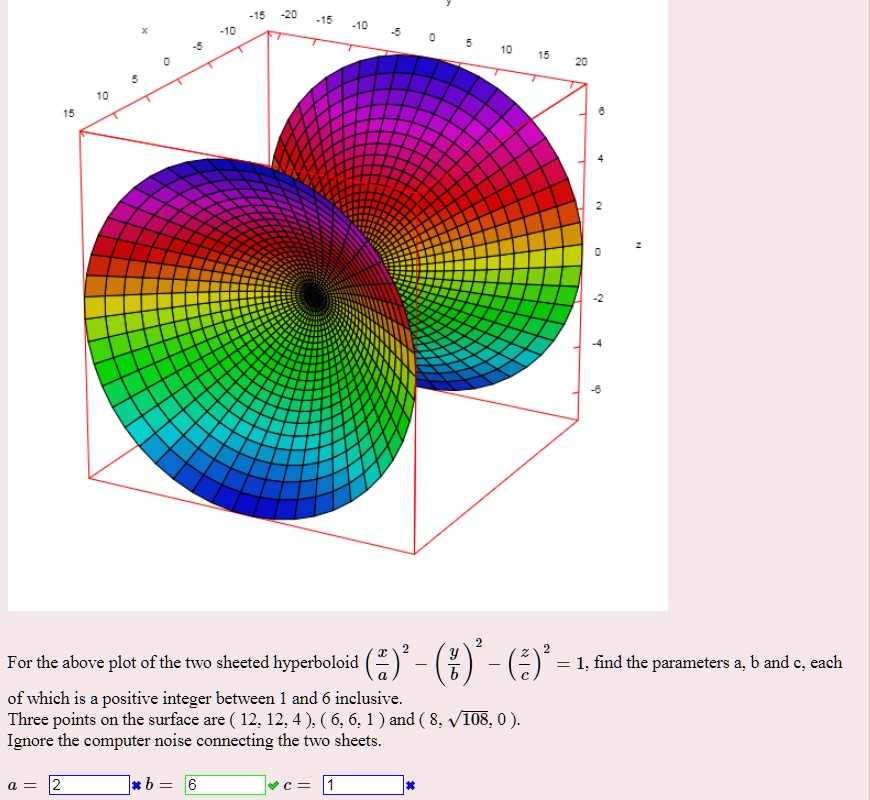
For the above plot of the twosheeted hyperboloid ("( ) (e)" = 1
All of its vertical cross sections exist — and are hyperbolas — but. For this reason, the surface is also called an elliptic hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. Is there a way to. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know.
Video 2960 Calculus 3 Quadric Surfaces Hyperboloid of two sheets
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. It’s a complicated surface, mainly because it comes in two pieces. For this reason, the surface is also called an elliptic hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is.
TwoSheeted Hyperboloid from Wolfram MathWorld
For this reason, the surface is also called an elliptic hyperboloid. Is there a way to. Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. All of its vertical cross.
It’s A Complicated Surface, Mainly Because It Comes In Two Pieces.
Let us say that we have a quadric equation, whose solution set lies in r3 r 3, and you know it's a hyperboloid. Is there a way to. If $a = b$, the intersections $z = c_0$ are circles, and the surface is called. For this reason, the surface is also called an elliptic hyperboloid.